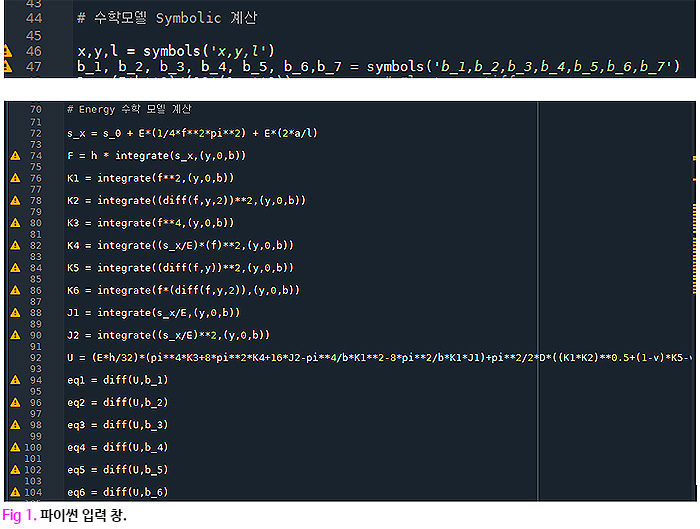
Fig.1 의 46번째 스크립트는 x,y와 b1,b2,b3 등을 Symbols란 함수로 정의하였습니다. 

여기서 'Symbols' 는 'Sympy'의 내장 함수이며 위 변수를 심볼로 정의하겠단 뜻을 의미합니다. 그리고 이러한 심볼을 기반으로 Fig. 5의 수식을 표현하였습니다. 주름 구조의 예측을 위하여 Ritz가 제안한 에너지 기반 방법론에 입각하여 수식을 세웠습니다.


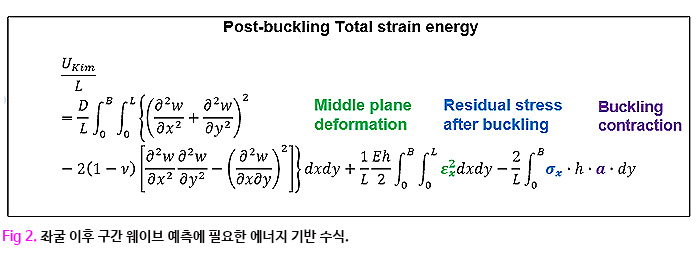
Fig. 1의 72번~104번 스크립트 까지는 Sympy라 하는 라이브러리를 통하여 위 수식을 정의하였습니다. 여기서 심볼릭으로 계산한 이유는 나중에 편미분을 해야만 하기 때문입니다. Sympy와 Numpy 모두 편 미분 계산을 할 수 있습니다. 하지만 출력 값의 차이가 존재합니다. 가령 y=x^2 라 하는 함수를 x에 대해서 미분을 하면 y=2x라는 값을 도출하기 위해서는 우리는 Sympy를 통해서 구하는 것이 적절합니다. 하지만 Numpy에서는 y=x^2란 함수를 x에대해서 미분이 되지 않습니다. Numpy는 수치 계산을 기반으로 합니다. x가 숫자로 정의되어 있지 않으면 연산이 되지 않습니다. 그러므로 y=2x라 하는 심볼릭 기반의 식을 도출할 수 없고 x=0 에서 미분 값, x=1에서 미분 값 등 이산적인 값을 도출할 수 밖에 없습니다.

심볼릭으로 정의된 b1,b2,b3와 x,y로 구성된 미지수 기반의 방정식을diff(U,b_1) 이란 편 미분 명령어를 통하여 각 계수별로 식을 얻어낼 수 있습니다. 기존 MATLAB 의 경우 풀어야 할 방정식이 명확히 존재하면 각 식들을 호출하여 적절한 솔버를 선택하여 해를 도출하면 되었으나 파이썬은 쉽게 되지 않았습니다. 위에서 말한 것처럼 계산은 Sympy에서 진행했고 솔버는 Sympy가 아닌 외부 라이브러리를 적용하려면 이에 맞게 변환을 해주는 과정이 필요합니다. 이 부분에 대한 해답을 얻기 위해서 좀 많은 고생을 했던 것 같습니다.


Fig. 3에서 사용된 명령어 lambdify는 Numpy와 Sympy를 변환해주는 명령어 입니다. 우리가 최종적으로 구한 eq1~eq6는 심볼릭 기반의 방정식들입니다. 해를 구하기 위해서는 Numpy 형태로 바꿔준 뒤 수치 계산을 진행해야만 합니다.

따라서 본인이 바꾸려고 하는 심볼릭 함수와 어떤 변수가 미지수인지 언급을 해줘 새로운 Numpy 형태의 식을 도출합니다. 이렇게 도출 된 식을 풀기 위해선 다양한 Solver들이 존재하는데 저는 비선형 연립 방정식에 특화된 Fsolve란 내장함수를 사용하여 문제를 풀었습니다.


파이썬, 매트랩을 기반으로 이론 모델을 구체화하였습니다. Pre-Buckling 을 통하여 구현한 결과는 논문상에 명확히 언급이 되어있기 때문에 결과를 검증하는데 무리가 없었습니다. 하지만 Post-buckling의 결과를 분석하기 위해 명확한 척도가 존재하지 않았습니다. 접근 하는 방법은 모두 Ritz 에너지 방법을 통하여 식을 정의하였으나 도출 된 식을 풀이하는 과정이 논문마다 다르고 가해주는 응력 분포 식도 달랐기 때문에 본인만의 검증할 수 있는 방법이 없다면 명확하게 확인할 수 없었습니다.


 

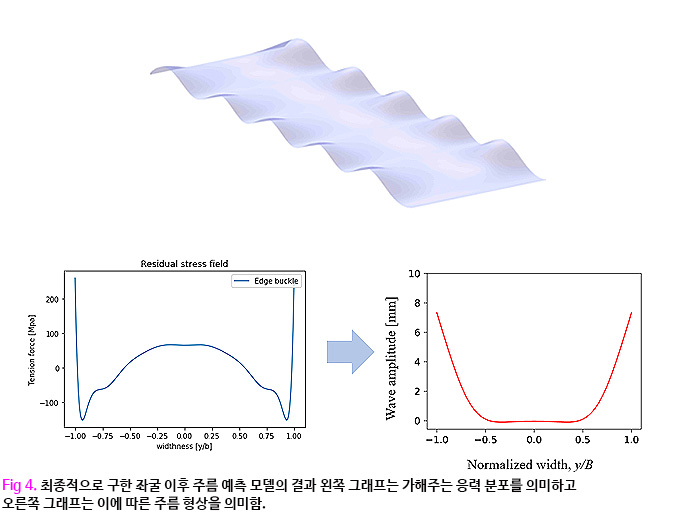
파이썬을 통해서 나온 결과는 위와 같습니다. 응력 분포를 왼쪽 그림과 같은 상태를 얇은 평판에 가해진다고 가정할 때 오른쪽 처럼 주름의 형상이 나오게 되었습니다.