지금까지 Pre-Buckling 해석을 위한 이론 모델을 구축하는 과정과 그 결과에 대해서 말씀드렸습니다. 하지만 주름 구조의 정확한 예측이란 것은 얼마나 주름이 생기고 그 주름은 어떤 형상으로 생기며 그 높이는 어느정도 되는 지와 같은 구체적인 사실을 알고 싶을 때는 Pre-Buckling 해석으로는 부족합니다. 앞에서 설명하였지만 Pre-Buckling 해석으로 알 수 있는 정보는 임계좌굴하중과 Eigen-Mode 입니다.
이는 언제 좌굴이 발생하는지와 만약 발생하게 된다면 웨이브가 어떤 모드로 생긴다란 정보만을 알려줍니다. 하지만 좌굴이 발생하고 난 뒤 웨이브의 형상을 예측하기 위해서는 Pre-buckling 해석으로 접근할 수 없습니다. 왜냐하면 Post-Buckling 구간에서 변형 정도가 매우 크기 때문에 비선형 거동 특성을 보이고 이론적인 접근이 때론 어긋나게 됩니다.
Fig. 1 그림을 참고하면 조금 더 명확하게 알 수 있습니다. Pre-Buckling 은 저희 눈에 안보일 정도로 변형이 작아서 실제로 관측되긴 힘들고 언제 좌굴이 시작되는지 시작 지점에 대한 정보를 알려줍니다. 이후 좌굴 과정이 충분히 발생되면 주름이 발생되는데 이 때부터 대 변형이 수반되고 거동이 비선형적으로 표현됩니다. 나뭇잎의 주름 구조나 피부의 주름과 같이 시각적으로 눈에 보일 수준의 정도는 어느정도 큰 변형이 수반된 것이고 Pre-Buckling 해석의 접근으로는 이들의 주름 정도를 알기에는 부족합니다.
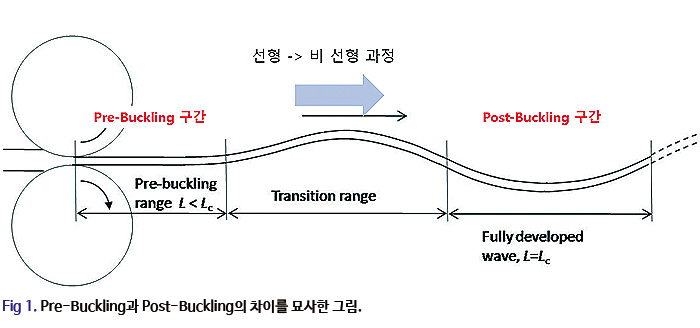
이런 경우에는 조금 개정된 Ritz-Galerkin 방법을 통하여 문제를 해결할 수 있습니다. Ritz-galerkin 법은 Ritz의 에너지 방법과 유사하지만 여기서 우리가 변수로 보는 것이 임계좌굴하중과 Eigen mode가 아닌 웨이브 형상을 결정짓는 특정한 상수와 파장으로 정의합니다.
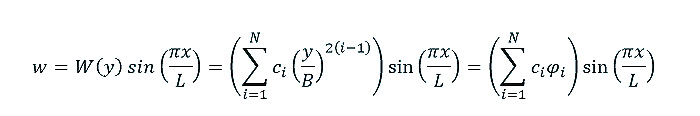
위 식이 의미하는 것은 주름 구조의 웨이브 식을 위와 같은 사인 함수와 다항식의 Expansion 형태의 곱으로 정의한다는 것입니다. 그렇게 되면 Post-Buckling에서 알아야 하는 미지수의 변수는 웨이브 형상을 결정짓는 미지수 ci 갯수(N)와 Wavelength (L) 으로 총 N+1개의 변수를 구해내야만 합니다. 또한 Pre-Buckling 해석에서는 Fig 7. 그림에서 알 수 있듯이 판의 처짐이 거의 없습니다.
반면 Post-Buckling의 경우 웨이브가 발생되는 것을 볼 수 있습니다. 다시 말하면 Pre-Buckling 같은 경우에 Mid-Plane의 에너지 변형을 포텐셜 에너지에 고려하지 않았지만 Post-Buckling에서는 반드시 이 변형에 의한 에너지를 추가적으로 고려해야만 합니다. 즉, 계산해야할 코스트가 증가한 것으로 볼 수 있습니다.
Pre-buckling의 경우 푸는 해는 겨우 2개 (임계 하중 응력, Eigen mode) 로 정의되어서 매우 간단하고 빠르게 해를 구할 수 있었습니다. 하지만 Post-buckling의 경우 풀어야 하는 해는 (주름 구조의 웨이브 높이와 관련된 변수 N개, 파장 1개)로 총 N+1개이고 에너지의 계산량이 증가하였기 때문에 더욱 복잡한 경우로 취급 됩니다.
열간 압연 공정 중 소재에서 발생되는 웨이브를 예측하는 Fischer의 논문을 기반으로 Pre-buckling 이론 모델을 구축한 방법과 그 결과에 대해서 말씀드렸습니다. 일반적으로 Pre-buckling 분석은 비교적 수월하게 진행이 되었고 결과 역시 논문과 매우 유사하기 때문에 결과에 대한 신뢰도를 얻을 수 있었습니다.
Post-Buckling 해석에 대해서 다음편에 얘기를 해보려고 합니다. MATLAB과 달리 파이썬 프로그래밍을 통하여 이론 모델을 구축하였기 때문에 파이썬에 관심이 있으신 분들은 한번 읽어보시면 도움이 될 것 같습니다. 추가로 Pre-Buckling과 달리 Post-Buckling에서는 이론 모델의 검증을 하기 위한 논문 레퍼런스가 존재하지 않아서 직접 해를 검증하는 별도의 수단을 구축해야만 하였습니다.
저는 유한요소해석 시뮬레이션을 도입하였고 이론 결과와 비교 분석을 통하여 연구를 진행하였습니다. 따라서 파이썬을 통한 수식 모델링과 유한요소해석을 통한 검증으로 다음 편에서 그 내용을 공유하고자 합니다.


|






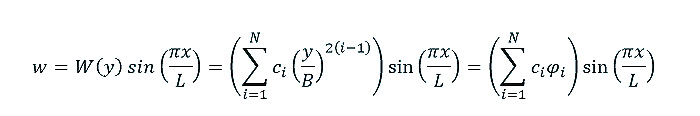




.jpg)
.jpg)





(0).jpg)















