MATLAB이란 상용프로그램을 활용하여 위와 같은 이론 모델을 직접 수행해 보았습니다. 학부 시절에 MATLAB에 대해서 가볍게 다뤘지만 중급 이상의 코스를 배우기 위해서는 별도의 학습이 필요하였습니다. 저는 https://kr.mathworks.com/ 란 공식 사이트에 일련의 예제와 문제를 푸는 방식들을 기반으로 실력을 키웠습니다.

저는 MATLAB을 사용하여서 Fischer가 제안한 Pre-Buckling 해석을 한번 따라해보았습니다. 기본적으로 Pre-Buckling 해석은 고유치 문제(Eigen-Value Problem)으로 수식을 전개하게 됩니다. 고유치 문제(EVP)는 고체역학 뿐만 아니라 진동 공학 등 넓은 범위의 공학 분야에서 다뤄지기 때문에 누구나 한번 쯤은 들어봤을 것입니다.
고유치 문제를 풀기 위해서는 일련의 지배 방정식이 필요하는데 얇은 평판의 변형 정도와 관련된 지배 방정식은 일반적으로 4차 편미분 방정식으로 정의됩니다. 이는 Foppl-Von Karman equation이라하는 사람이 제안한 모델로서 직접 해를 구하는 것이 매우 어렵습니다.
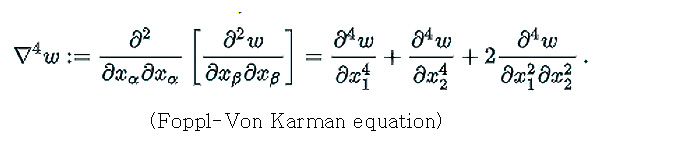
위 수식에서 w 가 의미하는 것은 횡 방향으로의 변위를 의미합니다. 이 방정식을 직접 푼다는 것은 어렵기 때문에 고체역학에서는 Ritz가 제안한 에너지 방법을 이용하게 됩니다. 에너지 방법이란 것은 구조물이 가지고 있는 초기의 포텐셜 에너지와 어떤 외부 하중에 의하여 변형이 발생했을 때의 포텐셜 에너지의 차이 값이 변위에 대하여 항상 최소화되는 방향으로 진행한다는 원리입니다. 원리를 적용하기 위해서는 평판의 변형 에너지가 무엇인지 알아야만 합니다.
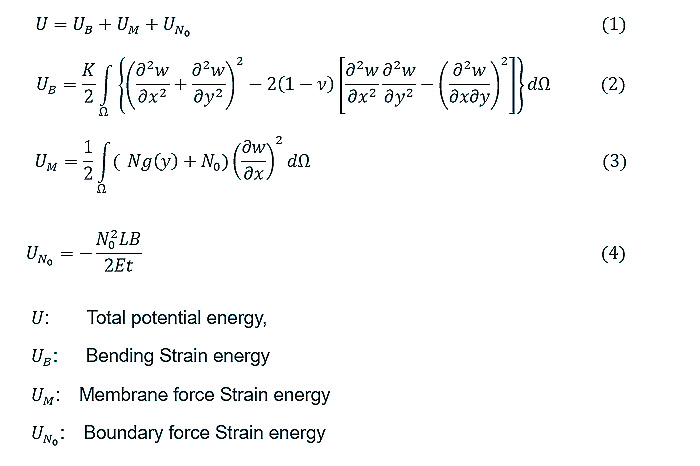
평판이 갖는 변형 후 에너지는 위에서 언급한 것처럼 4 가지의 형태의 에너지의 합으로 고려됩니다. 따라서 Ritz의 에너지 최소화 이론은 위 포텐셜 에너지를 변형 후의 변위를 미지수로 가정하여 편 미분을 한 뒤 여러 개의 방정식을 대수적으로 푸는 것입니다. 이 방법을 적용한다면 기존의 편 미분 방정식이 대수적 방정식으로 문제가 바뀌기 때문에 접근방법이 매우 용이합니다. 얇은 평판의 Pre-Buckling 해석을 위하여 일련의 수식적 작업을 MATLAB 으로 표현하였고 이를 기반으로 해를 도출하였습니다.


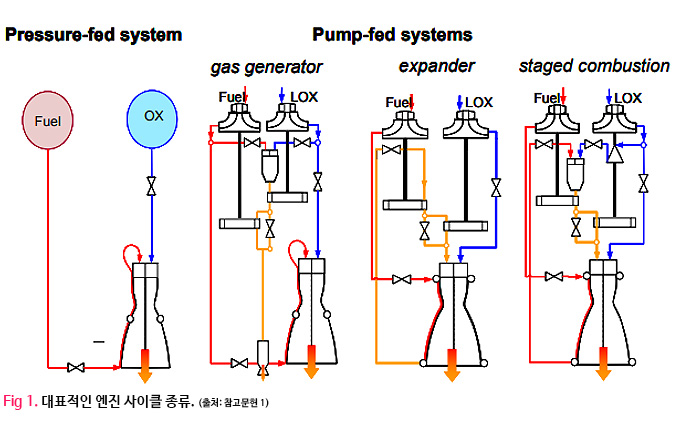
Fig 1. 는 MATLAB을 기반으로 수식화 과정을 편집한 스크립트를 보여줍니다. 기본적인 적분과 미분의 수식은 기본 가이드라인으로 부터 구현할 수 있었지만 해를 구하는 방법론에서 많이 막혔습니다. 즉 기본적으로 풀어야 하는 방정식을 얻었지만 이 방정식을 제대로 풀기 위해서는 전문가의 조언과 어떤 솔버를 적용해서 풀어야 하는지 세부적인 정보가 필요하였습니다.
여기서 https://stackoverflow.com/ 란 사이트를 통해서 해결했습니다

세계적으로 코딩과 관련된 내용을 주고받는 국제 커뮤니티라고 보시면 됩니다. 이 사이트 최고의 장점은 다른 사람들이 공유한 코딩 파일을 다운받을 수도 있고 스크립트를 통하여 연구에 직접 적용할 수 있습니다. 저 같은 경우에 기본적인 수식을 구성하는 방법은 완성은 하였지만 올바른 해를 검출하기 위해 어떤 솔버로 어떻게 문제를 풀어야 할지 막막하였습니다. Stackoverflow란 사이트에서 이를 해결할 수 있었습니다.
영어로 적어야 된다는 단점을 빼고 현재 직면한 문제에 대해서 상세하게 서술하여 글을 올렸더니 정말 빠르게 도와주었습니다. 칼텍에 다니는 수학과 학생이 직접 코딩을 짜주고 이런 문제가 있었고 이렇게 해결하면 된다라는 답변을 달아주었습니다. 물론 본인 스스로 해결하는 습관은 중요하지만 최대한 노력을 해본 뒤 이런 공유사이트에서 고충을 털어 놓는 것 도 좋은 방법이 아닐까 싶습니다.
결과적으로 수식 모델을 구축하는데 성공하였습니다. 여기서 중요한 것은 구성한 결과가 실제 논문과 비슷하게 나왔는지 확인을 하는 과정이 중요합니다. 따라서 저는 논문에서 제시된 총 3가지의 경우를 확인해 보았습니다.
여기서 추가적인 설명을 드리면 Pre-Buckling 모델의 경우 기본적으로 예측할 수 있는 것은 Eigen-Mode와 임계 좌굴 하중(Critical Buckling Load) 입니다. 임계 좌굴 하중은 이 이상의 하중을 가할 때 좌굴이 발생되고 주름 구조를 형성하는 기준점이 됩니다. 그리고 이 때 발생되는 주름의 구조 형태가 어떤 모드를 갖는다면 그 모드를 Eigen-mode라고 합니다. 저는 수식 모델을 비교할 때 이 두 가지의 변수의 결과 값을 비교하였습니다.
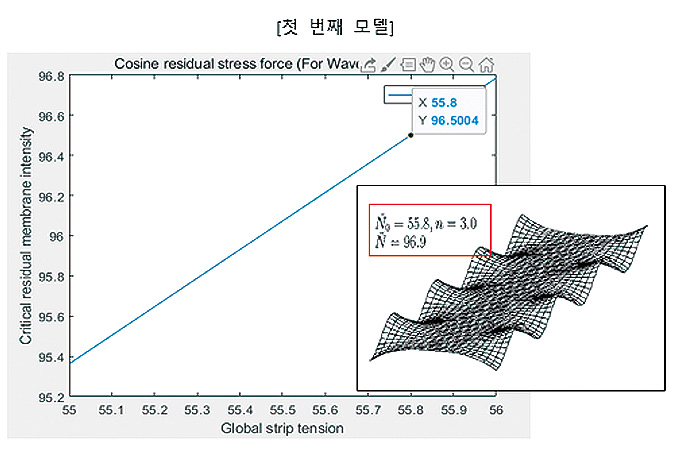
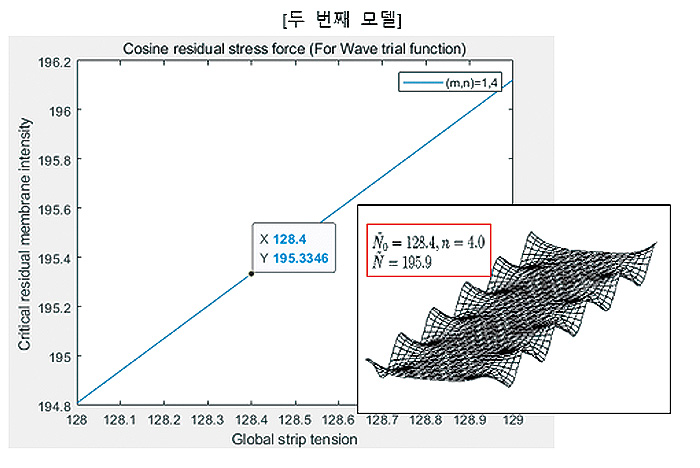
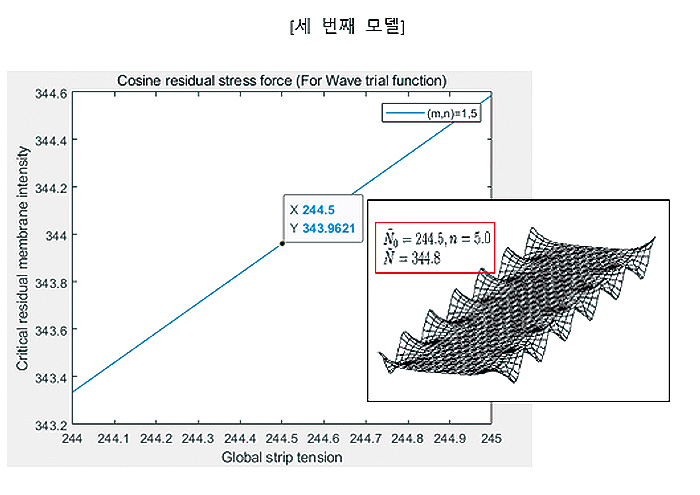
위의 3가지 경우는 제가 실제로 MATLAB 코딩을 진행해서 나온 결과와 논문에서 나온 결과를 비교한 것입니다. 거의 3 가지 모두 경우 일치하는 것을 알 수 있었습니다. 연구를 진행함에 필요한 과정인 이론 모델 구축을 위하여 저는 MATLAB과 StackOverflow라 하는 웹사이트로부터 도움을 많이 받게 되어 문제를 해결할 수 있었습니다. Pre-Buckling 이론 모델링을 성공적으로 구축하였습니다만 Post-Buckling의 경우 문제가 더 복잡해집니다.
 
|






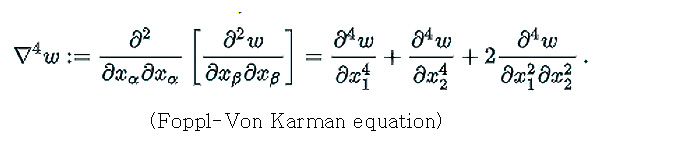
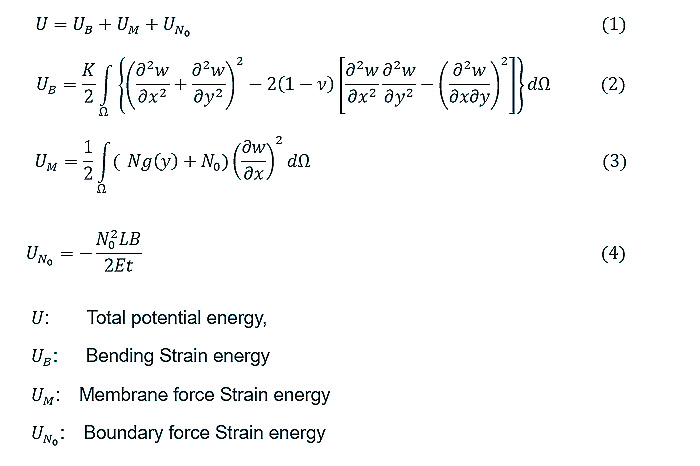










.jpg)
.jpg)





(0).jpg)















