|
현실적인 공학 문제는 고차원 데이터를 도출하는 고해상도 실험 또는 계산을 실시간 또는 여러 번 반복해서 수행하는 경우가 많이 있습니다.
이번 서면 인터뷰에서 만나 보실 이경훈 교수(부산대학교 항공우주공학과)는 축소기저를 사용한 편미분 방정식의 신속 정확한 해석을 실시간(예를 들어 디지털 트윈) 또는 반복 해석(예를 들어 확률론적 최적 설계)이 요구되는 공학 문제에 적용하고 있습니다. 최근 각광받는 머신 러닝을 활용해 축소기저 해석의 사후오차 분석을 개선하는 연구 및 대규모 구조물의 신속 정확한 디지털 트윈을 개발하는 연구를 하고 계시는데요. 연구에 대한 자세한 이야기해보도록 하겠습니다.
1. 현재 교수님께서 하고 계시는 주요 연구에 대한 간단한 소개 부탁드립니다.
저희 연구실에서는 데이터/물리 정보에 기반하여 신속 정확한 예측 모형을 구성하고 이를 다양한 공학 문제에 응용하는 연구를 하고 있습니다. 가우스 과정(Gaussian process regression) 기법으로 데이터에 기반한 예측 모형을 만드는 연구는 Fig 1-A 같이 6자유도 공력계수 데이터를 사용해서 수행하고 있습니다.
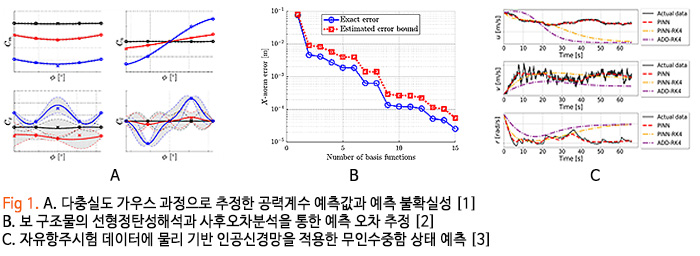
편미분 방정식에 기반하여 축소기저법(reduced basis method)으로 예측 모형을 만드는 연구는 Fig 1-B와 같이 선형정탄성 구조해석을 사용해서 수행하고 있습니다. 데이터 및 물리 정보 모두를 활용하는 물리 기반 인공신경망(physics-informed neural network) 기법을 사용하여 Fig 1-C 같이 무인수중함의 상태 및 유체력을 예측하는 연구도 수행하고 있습니다.
2. 축소기저법 및 정적응축 축소기저요소법에 대한 자세한 설명 부탁드립니다.
축소기저법은 매개변수화된 편미분 방정식(parameterized partial differential equation)의 신속 정확한 해석을 위해 고안된 기법입니다. 일반적으로 다양한 공학 문제는 물리 법칙의 지배를 받는 시스템의 거동을 실시간 또는 반복적으로 예측하는 문제로 정형화 될 수 있고 축소기저법은 이런 문제를 기존 유한요소법에 비해 효과적으로 해결할 수 있습니다.
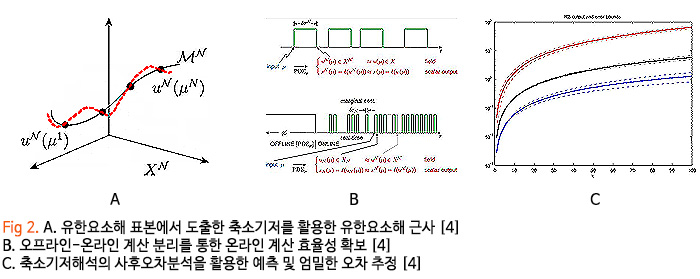
많은 공학 문제에는 변경하고 싶은 매개변수(예를 들어 물성치나 운용조건)가 존재하고 이런 매개변수의 변화는 어느 정도의 범위가 사전에 정해져 있습니다. 이렇게 매개변수의 개수와 변동폭이 주어진 물리 시스템을 지배하는 편미분 방정식의 수치해는 Fig 2-A와 같이 기존 유한요소기저보다 훨씬 적은 수의 축소기저를 사용해서 효과적으로 근사가능합니다. 특히 축소기저해석은 Fig 2-B에 나타나듯 오프라인-온라인 계산 분리를 통한 계산 효율성을 추구하여 온라인 단계에서는 유한요소해석보다 훨씬 빨리 편미분 방정식의 수치해를 근사할 수 있습니다. 무엇보다도 Fig 2-C와 같이 사후오차분석(a posteriori error analysis)을 통해 축소기저근사의 오차를 수학적으로 정량화 가능하여 유한요소해의 도움없이 축소기저해의 정확도를 점검할 수 있는 장점이 있습니다.
다만 매개변수의 개수가 많아지거나 변동폭이 커질 경우 축소기저 개수 또한 증가하여 축소기저해석의 효율성이 떨어지기 쉬운데 이런 한계를 극복하기 위해 정적응축 축소기저요소법(static condensation reduced basis element method)이 개발되었습니다. 정적응축 축소기저요소법은 하나의 물리 시스템을 여러 컴포넌트로 분할한 후 각 컴포넌트 해석에 축소기저법을 적용하기 때문에 매개변수의 개수가 많은 대규모 물리 시스템의 해석을 신속하되 정확히 수행할 수 있습니다.
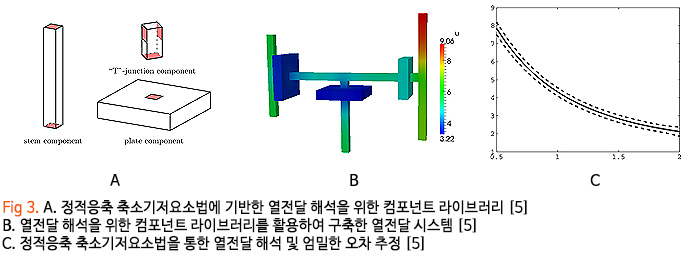
예를 들어 Fig 3-A 같이 열전달 시스템을 구성하는 컴포넌트 라이브러리를 구성한 후 다양한 조합을 통해 Fig 3-B 같이 여러 형상의 열전달 시스템을 즉석에서 구성하여 해석 가능합니다. 축소기저법처럼 사후오차분석도 가능하여 Fig 3-C 같이 근사 오차를 엄밀히 정량화할 수 있습니다. 다만 선형성에 기초하여 편미분 방정식을 나누어 다루기 때문에 선형 편미분 방정식에만 적용 가능하다는 한계가 있습니다. 비선형 거동이 포함된 물리 시스템의 경우 비선형 영역만 따로 분리하여 나머지 선형 영역에만 적용 가능합니다.
3. 축소기저법이나 정적응축 축소기저요소법을 사용하여 기존 유한요소법에 비해 편미분 방정식의 해를 효율적으로 도출할 수 있다고 하는데요. 유한요소법과 차이점이 많이 큰가요?
기본적으로 축소기저법과 정적응축 축소기저요소법은 편미분 방정식의 약형을 다룬다는 점에서 유한요소법과 같습니다. 다만 매개변수의 변화에 따른 편미분 방정식의 수치해를 신속 정확하게 구하고자 하기 때문에 이를 위해 약형을 재구성하며 계산 과정이 Fig 2-B 같이 오프라인-온라인으로 구분되는 점이 다릅니다. 오프라인 단계에서는 매개변수와 상관없는 행렬과 벡터를 한번만 계산하여 저장해둔 후 축소기저공간을 구성하는 기저 함수를 유한요소해를 바탕으로 도출합니다. 온라인 단계에서는 매개변수에 따라 변하는 항을 계산한 후 축소기저공간 상에서 약형을 재조합해서 근사해를 도출합니다. 즉, 오프라인 계산 비용을 미리 지불해서 온라인 계산을 빠르게 수행하는 점이 유한요소법과 가장 큰 차이입니다.
4. 무엇보다 축소기저법과 정적응축 축소기저요소법은 축소기저로 인한 해석 오차를 사후오차분석을 통해 정량화할 수 있다고 하는데요. 사후오차분석에 따른 오차 추정이 실제 오차 대비 어느 정도 정확한지 궁금합니다.
축소기저법 및 정적응축 축소기저요소법은 수학적으로 엄밀한 사후오차분석이 가능합니다. 이러한 사후오차분석을 활용한 축소기저법 및 정적응축 축소기저요소법을 “보증된” 축소기저법 및 정적응축 축소기저요소법이라고 부르기도 합니다. 왜냐면 유한요소해석 대비 축소기저해의 오차 상한을 제시하여 실제 오차가 오차 상한보다 항상 작음을 “보증”할 수 있기 때문입니다. 무엇보다도 오차 상한 계산에 유한요소해석이 필요하지 않아 사후오차분석을 온라인 단계에서 빨리 수행할 수 있습니다.
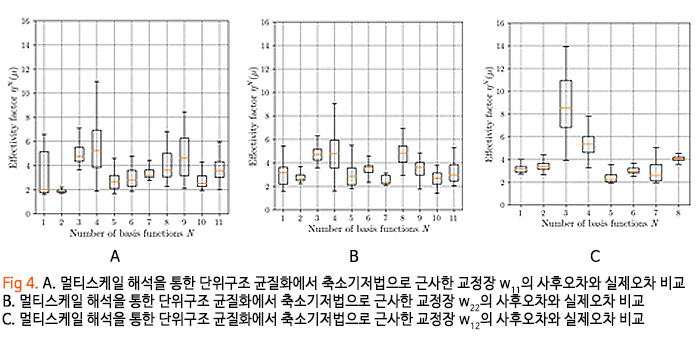
타원형/포물선형 편미분 방정식의 경우 사후오차분석에 따른 오차 추정은 실제 오차에 비해 보통 O(10) 정도를 보여줍니다(예를 들어 실제 오차가 1이라면 오차 추정은 10). 예를 들어 Figs 4는 멀티스케일 해석을 통한 균질화 문제에 축소기저법을 적용하여 근사한 교정장 대비 유한요소법으로 구한 실제 교정장의 비교를 보여 줍니다. 모든 값이 O(10)을 나타내어 실제 오차에 비해 사후오차분석으로 추정한 오차가 그리 과장되지 않음을 알 수 있습니다. 하지만 쌍곡선형 편미분 방정식의 경우 사후오차 분석에 따른 오차 추정이 실제 오차에 비해 너무 커서 실용성이 낮아 사용하지 않습니다. 정적응축 축소기요소법 역시 사후오차분석이 가능한데 일반적으로 같은 문제에 대해 축소기저법을 적용한 경우보다는 조금 더 과장된 오차 추정을 보여줍니다. 마지막으로 수학적으로 엄밀한 사후오차분석이 모든 문제에 항상 가능한 것은 아니지만 실용적인 측면에서 수학적 엄밀성을 포기하면 여전히 활용 가능합니다.
5. 연구하신 분야의 국내 상황과 국외 상황을 구체적으로 비교해주신다면 어떤 실정인가요.
국내에 기존 차수축소법(model order reduction)을 연구하시고 사용하시는 분들은 여러 공학 분야에서 많습니다. 하지만 축소기저법과 정적응축 축소기저요소법을 연구하고 활용하시는 분은 거의 없다고 알고 있습니다. 특히 사후오차분석과 관련된 연구는 전무합니다. 이에 비해 국외에서는 MIT의 Patera 교수님을 중심으로 한 연구 그룹이 미국과 유럽에서 이 분야 연구를 주도하고 있습니다. 저도 정규직교분해(proper orthogonal decomposition, POD)에 기반한 차수축소법을 연구하다가 Patera 교수님 연구 그룹을 통해서 2011년에 축소기저법과 사후오차분석을 처음으로 접했습니다. 사후오차 분석이 가능한 축소기저법과 정적응축 축소기저요소법은 편미분 방정식의 해를 신속 정확히 도출하는데 탁월한 기법입니다. 국내에도 관련 연구자가 많아져서 산업체의 현장에서 대두되는 여러 다양한 문제를 해결하는데 도움이 되었으면 좋겠습니다.
6. 축소기저법과 정적응축 축소기저요소법의 방법론과 관련해서 수행하신 연구가 있으신가요.
축소기저해석의 사후오차 분석과 관련하여 기계학습을 적용하는 연구를 수행하고 있습니다. 사후오차분석에 따른 오차 상한을 계산하기 위해서는 안정상수(stability constant)를 구해야 되는데 일반화된 고유치 문제를 다루어야 해서 온라인에서 직접 계산할 수 없습니다. 기존에는 SCM(successive constraint method)이 제안되어 온라인에서도 신속한 안정상수 하한 도출이 가능해졌습니다. 하지만 기하변환을 고려한 선형 정탄성 문제 같이 특정 문제의 경우 SCM으로 도출한 안정상수 하한이 안정상수에 근접하지 못해 사후오차를 과대추정하는 문제가 있습니다.
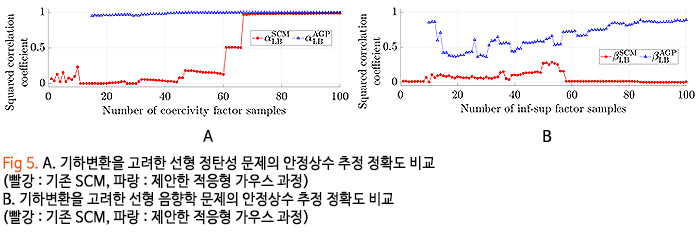
이를 극복하기 위해 기계학습의 예측 불확실성에 기반한 안정상수 하한을 도출하는 방법을 제안하여 기존 SCM 대비 사후오차 분석의 엄밀성, 정밀성, 효율성을 제고하려는 연구를 수행중입니다. Figs 5에서 보듯이 저희가 제안한 기법이 기존 SCM에 비해 안정상수 표본의 추가에 따라 실제 안정상수를 더 정확히 근사함을 알 수 있습니다.
7. 수행하신 기계학습 기반 축소기저해석의 사후오차분석 관련 연구에 대한 보완해야할 점은 없는 건지 궁금합니다.
매개변수 변화에 따른 안정상수의 변화를 살펴보면 매개변수에 대해 연속이나 미분 불가능한 영역이 존재합니다. 기계학습으로 안정상수를 예측하는 모형을 만들면 이러한 미분 불가능한 영역을 잘 따라가지 못하여 기계학습 예측 모형의 정확도가 낮아지는 문제가 있습니다. 미분 불가능한 안정상수 변화를 잘 예측할 수 있는 기계학습을 찾거나 아니면 직접 고안하는 연구가 필요합니다.
8. 정적응축 축소기저요소법을 활용하여 다양한 날개 구조물을 표현하고 해석할 수 있다고 하는데요. 구체적으로 어떤 분야에서 활용 가능한가요?
시스템을 컴포넌트로 나누어 표현 가능한 정적응축 축소기저요소법을 사용하면 Fig 6와 같이 단지 4개의 공통된 컴포넌트를 가지고 날개 형상 변수를 적절히 변경하면서 여러 날개 형상을 즉각적으로 재구성하고 동시에 선형 정탄성 해석을 근실시간(near real-time)으로 수행할 수 있습니다.
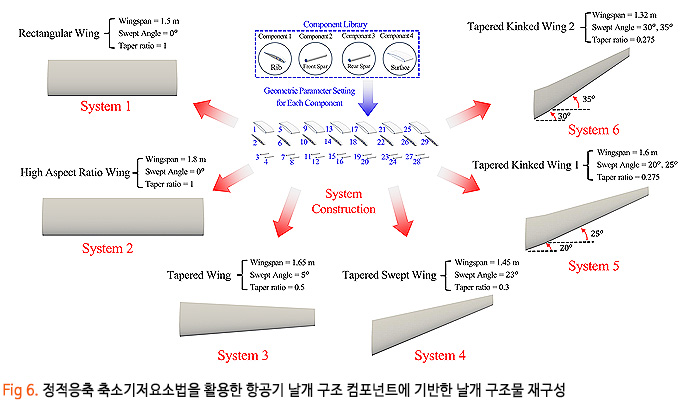
이러한 해석 능력은 항공기 날개 구조물의 예비 설계(preimary design)에 상당히 효과적입니다. 또는 항공기 날개 구조물의 디지털 트윈을 구현할 수 있어 항공기 운용 중 손상에 따른 디지털 트윈의 즉각적인 재구성도 가능합니다.
9. 2003년부터 조지아 공과대학 (Georgia Institute of Technology)에서 석박사 후 연구원으로 재직하고, 2011년도 SUTD-MIT International Design Centre(IDC)에 계셨는데요. 그 당시 어떤 연구를 하셨는지 궁금합니다.
조지아 공과대학에서는 확률론적 정규직교분해를 이용한 차수축소법을 연구하였습니다.
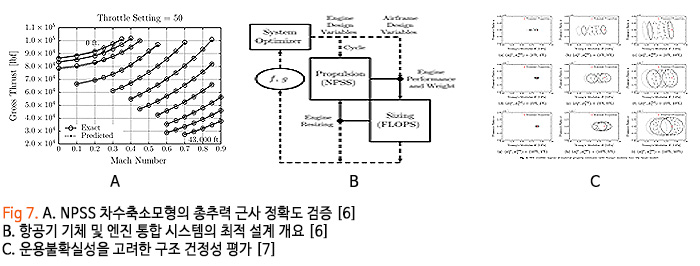
연구 결과를 추진기관 해석도구인 NPSS(numerical propulsion system simultion)에 적용하여 Fig 7-A 같이 축소기저모형을 만든 후 Fig 7-B에서 보듯이 항공기 기체 및 엔진 통합 시스템 설계를 수행하였습니다. 이후 SUTD-MIT IDC에서는 축소기저법을 사용하여 구조물 거동 예측 모형의 오차를 연속 균등 분포로 모델링한 후 Fig 7-C과 같이 운용 불확실성을 고려한 구조 건정성 평가를 신속 정확하게 수행하는 연구를 진행했습니다.
10. 연구 진행 중 어려운 점이 있었다면 어떤 점이었으며, 어떻게 해결해 오셨는지 알려주세요.
연구 중인 문제가 해결이 어려운 경우는 잠시 휴식을 가지면서 틈틈이 문제를 복기하면서 놓치는 부분이 없는지 처음부터 하나하나 점검해봅니다. 복잡한 문제를 직접 다루기보다는 문제의 특징을 나타내는 간단한 예제를 만들어서 해당 문제를 해결해보려고 합니다. 비슷한 연구를 하는 동료 연구자들에게도 다방면으로 조언을 구합니다.

11. 수행하신 연구에 힘입어 앞으로 연구 계획 중인 연구나 또 다른 목표가 있으신지 궁금합니다.
현재 연구중인 기계학습을 활용한 축소기저해석의 사후오차분석을 정적응축 축소기저요소해석에도 적용할 계획입니다. 당분간은 정적응축 축소기저요소법을 사용한 디지털 트윈 구축에 집중할 계획입니다.
12. 앞으로 관련 분야를 공부하는 후학(대학원생들)에게 이 분야의 연구에 대한 비전을 제시해 주신다면.
편미분 방정식의 수치해를 신속 정확하게 근사하는 축소기저법과 정적응축 축소기저요소법은 디지털 전환을 가능하게 해주는 중요한 기술입니다. 산업계의 디지털화가 진행되면서 많은 수요가 있으리라 생각합니다.
|


